今年の高校入試では、四分位数や四分位範囲を求める問題や、箱ひげ図を求める問題が出ました。
古い記憶のかなたに追いやられている私の中学時代、そういったことは習っていません。
それは、おそらく確かなことです。
いくら記憶がとおくなったとしても、きっとそうです。
さて、いったいそれらは、何なんでしょう。
じつは、エクセルでも簡単に導き出すことができます。
たとえば、こんなデータがあります。あったんです。
82, 64, 72, 74, 94, 77, 85, 88, 97
これは、なんでもいいのですが、ある試験の点数としましょうか。
9人分です。
まずは、値が小さい順に並べましょう。
すると・・
64, 72, 74, 77, 82, 85, 88, 94, 97
これで、以下の順に見ていきましょう。
1.最小値:64
2.最大値:97
3.中央値:82
ここまでは、いいでしょうか。
ここで、一つ言葉を覚えてください。
この、中央値を、第2四分位数と呼びます。
つぎに、中央値の下の4つのうちの中央値を出しましょう。
今回は、偶数ですから、中央の2つの平均値です。
これが、第1四分位数で、73になります。
つぎに、82より上にある4つのうちの中央は、88と94の平均です。
これが、第3四分位数で、91となります。
以上をまとめると、小さい順に・・・
1.最小値:64
2.第1四分位数:73
3.第2四分位数:82
4.第3四分位数:91
5.最大値:97
こんな感じですね。
これを、図に表したものが、箱ひげ図となります。
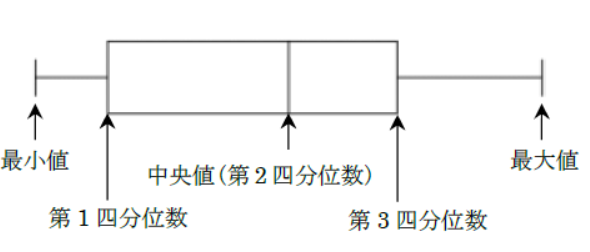
それでは、エクセルに描いてもらいましょう。
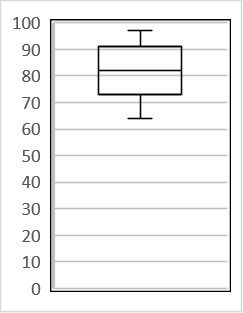
いかがでしょうか。
まぁ、自分で書いてもいいのですが、試しにエクセルの力を借りてみました。
忘れるところでした。
もうひとつ、大事な言葉として「四分位範囲」というのがあります。
これは、第3四分位数から第1四分位数を引いたものです。
それだけです。
さて、これがどんな形で、高校入試に出題されるかというと・・
中央値とか、四分位範囲とかきいたり、グラフ的な特徴をきくことが多いようですね。
よくありそうなものとしては、いくつかの特徴的な箱ひげ図を並べて、数値の散らばり具合をたずねるなんてことがありますね。
いくつかの入試問題を見ると、だいたい傾向がつかめます。ご安心を。
